Metoda najmniejszych kwadratów ( mnk )

Najlepiej znaną i najczęściej stosowaną w praktyce metodą estymacji
nieznanych parametrów strukturalnych
modelu
jest metoda najmniejszych kwadratów (MNK). Przyjmujemy następujące założenia
dotyczące stosowalności MNK do szacowania wektora
w modelu :

(Z1) zmienne objaśniające
są nielosowe i nieskorelowane ze składnikiem losowym ,

(Z2) rz(x)=k+1n,

(Z3) E=0,

(Z4) ,
przy czym

Niekiedy przyjmuje się dodatkowe założenie (Z5), rozszerzające założenia
(Z3) i (Z4) , mianowicie

(Z5)
dla t=1,2,…,n

Założenie (Z5) oznacza, że składnik losowy w każdym z okresów ma rozkład
normalny o wartości oczekiwanej 0 i skończonej, stałej wariancji
Zasadność założenia (Z2) ma charakter algebraiczny i zostanie wyjaśniona
poniżej. Założenia (Z3) i (Z4) warunkują korzystne własności
estymatora a wektora parametrów
wymienione w podanym dalej twierdzeniu Gaussa-Markowa. Symbolużyty
w twierdzeniu Z4 oznacza macierz wariancji i kowariancji wektora składników
losowych.

Założenia (Z1)-(Z4) dotyczące modelu
nazywane są założeniami klasycznej metody najmniejszych kwadratów, a MNK przy
tych założeniach określa się mianem klasycznej metody najmniejszych
kwadratów (KMNK).

METODA NAJMNIEJSZYCH KWADRATÓW ( MNK )

Zamierzamy wyznaczyć oceny a nieznanych
parametrów
modelu
. Wartości zmiennej objaśnianej otrzymane przy ocenach a
nazwiemy wartościami teoretycznymi zmiennej objaśnianej, oznaczymy je przez i
obliczymy jako:

t=1,2,…,n
(2.4)

Resztą dla okresu t nazwiemy różnicę między wartością
empiryczną a teoretyczną zmiennej objaśnianej , czyli

t=1,2,…,n
(2.5)

wartości teoretyczne zmiennej objaśnianej oraz reszty możemy
zapisać w postaci wektorów:

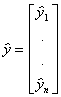
oraz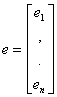

Wobec tego otrzymujemy macierzowy zapis równań (2.4)

(2.6)

oraz równań (2.5)

(2.7)

Idea metody najmniejszych kwadratów (MNK) polega na wyznaczenia
takiego wektora oszacowań a wektora parametrów, przy którym funkcja S(a) =
osiąga minimum . Funkcja S(a) wyraża sumę kwadratów odchyleń
teoretycznych wartości zmiennej objaśnianej od empirycznych wartości tej
zmiennej i może być przedstawiona w postaci

(2.8)

Poszukiwanie punktu stacjonarnego funkcji S z warunku
koniecznego istnienia ekstremum funkcji,

prowadzi do równania macierzowego

(2.9)

a w konsekwencji do układu równań normalnych względem
a postaci

(2.10)

Macierz
jest macierzą Grama dla macierzy X. Łatwo zauważyć
,że macierz jest kwadratową, symetryczną macierzą stopnia k+1.Warunek
konieczny i dostateczny na to , by macierz
była nieosobliwa jest identyczny
z założeniem (Z2). Widzimy więc że założenie (Z2) ma charakter
algebraiczny i warunkuje otrzymanie jedynego rozwiązania układu (2.10).

Przy założeniu (Z2) układ równań normalnych (2.10) jest więc
układem Cramera .Jego (jedyne) rozwiązanie dane jest wzorem

(2.11)

Można sprawić ,że macierz drugich pochodnych cząstkowych
funkcji S względem a jest równa

(2.12)

Jest ona dodatnio określona. Wobec tego funkcja S w punkcie a
osiąga minimum lokalne.

Gdy macierz X i wektor y mają znaną postać liczbową, wówczas
ze wzoru (2.11) otrzymamy oceny parametrów szacowanego modelu. W ogólnym
przypadku wzór (2.11) przedstawia postać estymatora parametrów modelu
wyprowadzono przy użyciu MNK z jedynym założeniem (Z2).Mimo identycznego
symbolu a stosowanego w statystyce i ekonometrii do oznaczenia estymatora i jego
konkretnej wartości (czyli oceny nieznanego parametru) nie należy mylić tych
dwóch pojęć.

 

Twierdzenie (Gaussa-Markowa)Estymator a wyznaczony KMNK jest estymatorem: liniowym , zgodnym, nieobciążonym i najefektywniejszym w klasie liniowych i nieobciążonym estymatorów wektora parametrów modelu .

 

 

 

Przypomnijmy, że:

– estymator zgodny jest zbieżny stochastycznie do ;

– estymator nieobciążony to taki ,dla którego E(a) = ;

– estymator najefektywniejszy ma w określonej klasie estymatorów
najmniejszą wariancję;

– estymator liniowy – uzasadnienie znajduje się poniżej.

Wektor a jest estymatorem liniowym, ponieważ każda składowa
wektora a jest liniową funkcją składowych wektora y
o współczynnikach z iloczynu .

Wektor mnk :

Wyznaczenie wektora ocen a za pomocą mnk jest tożsame z
wyznaczeniem pewnej hiperpłaszczyzny w przestrzeni .Odnotujemy niektóre
algebraiczne własności wektora a wyznaczonego przy użyciu MNK. Przyjmiemy
przy tym oznaczenie dla kolumnowego wektora jedynek

(2.13)

(2.14)

(2.15)

(2.16)

(2.17)

Procedura obliczenia wektora ocen a kończy etap estymacji
parametrów strukturalnych modelu ekonometrycznego.

Macierz kowariancji (niekiedy nazywana macierzą wariancji i
kowariancji estymatora a wyznaczamy ,korzystając z własności nieobciążności
estymatora a i z założenia (Z4), w podany sposób:

A zatem

(2.18)

Założenia klasycznej metody najmniejszych kwadratów (KMNK)

| METODA NAJMNIEJSZYCH KWADRATÓW | mnk