Metoda trendu pełzającego
Metoda ta jest numerycznym narzędziem wyodrębnienia tendencji rozwojowej zmiennej prognozowanej. Na wejściu zatem mamy n-elementowy szereg czasowy (okresów lub momentów) zawierający wartości empiryczne, a na wyjściu – również n-elementowy ciąg wartości teoretycznych. Procedurę postępowania w metodzie trendu pełzającego podzielimy na kroki, które koniecznie muszą być wykonane w przedstawionym porządku.
Krok 1. Arbitralne ustalenie wartości okresu wygładzania l.
Parametr l jest jedynym parametrem metody Hellwiga, którego nie szacujemy, lecz ustalamy go arbitralnie. Musi to być liczba naturalna, spełniająca dwa podstawowe warunki:
· (koniecznie!) 2 < l < n oraz
· l powinno być nieparzyste (3, 5, 7 itd.).
Warunek o nieparzystości nie musi być zachowany. Jeżeli jednak l będzie liczbą parzystą, to obliczone teoretyczne wartości zmiennej prognozowanej nie będą „trafiały” w indeksy (okresy lub momenty) odpowiednich empirycznych wartości tej zmiennej. Aby doprowadzić do niezbędnej zgodności indeksów t, trzeba wtedy obliczać średnie arytmetyczne wartości teoretycznych, co znacznie wydłuża proces obliczeń i naraża nas na dodatkowe błędy np. zaokrąglania.
Domyśla wartość parametru l (możliwie najmniejsza): l = 3. Jeżeli zatem brak jest jakichkolwiek wskazówek co do wartości l, wówczas należy przyjąć wartość domyślną. W praktyce, im mniejsze n, tym mniejsze l, i na odwrót. Pojemniejszy szereg czasowy pozwala nam zastosować większą wartość l i wtedy możemy uzyskać lepsze wygładzenie szeregu czasowego – teoretyczne wartości zmiennej prognozowanej łagodniej „pełzają” pomiędzy wartościami empirycznymi.
Krok 2. Oszacowanie k liniowych modeli tendencji rozwojowej
Parametr k oznacza liczbę liniowych modeli segmentowych.
k = n - l + 1
Jeżeli n = 15 a l = 5 to k = 11. Tyle właśnie 5-elementowych segmentów (podciągów) można utworzyć z macierzystego ciągu 15-elementowego. Każdy z szacowanych w tym kroku modeli segmentowych ma następującą postać (w zapisie pominięto składnik losowy):
yi(t) = ai + bi*t (i = 1, 2, ..., k oraz i £ t £ l+i-1)
gdzie:
i – numer modelu segmentowego,
yi(t) – teoretyczna wartość zmiennej prognozowanej dla okresu lub momentu t, obliczona na podstawie i-tego modelu segmentowego,
ai – parametr wolny i-tego modelu segmentowego,
bi – parametr związany ze zmienną czasową i-tego modelu segmentowego.
Jeżeli szereg czasowy składa się z n obserwacji na zmiennej prognozowanej
y1, y2, ..., yn-1, yn
to na wejściu procedury szacowania parametrów k modeli segmentowych mamy dane liczbowe wymienione w kolumnach 2 i 3 poniższej tabeli.
|
i |
Wartości zmiennej czasowej (t) |
Wartości empiryczne i-tego modelu (yt) |
Model do szacowania |
|
1 |
1, 2, ..., l |
y1, y2, ..., yl |
y1(t) = a1 + b1*t |
|
2 |
2, 3, ..., l+1 |
y2, y3, ..., yl+1 |
y2(t) = a2 + b2*t |
|
... |
... |
... |
... |
|
k-1 |
n-l, n-l+1, ..., n-1 |
yn-l, yn-l+1, ..., yn-1 |
yk-1(t) = ak-1 + bk-1*t |
|
k |
n-l+1, n-l+2, ..., n |
yn-l+1, yn-l+2, ..., yn |
yk(t) = ak + bk*t |
Dla każdego modelu segmentowego (i) oceny parametrów ai, bi obliczamy, stosując dowolne z wymienionych poniżej podejść (sposobów):
- Sposób klasyczny ("macierzowa" MNK – wzory znane z kursu ekonometrii)
![]()
gdzie:
a
– wektor kolumnowy ocen parametrów strukturalnych,
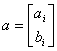 ,
,
X – macierz obserwacji na zmiennych niezależnych, i tak (gdy l = 3):
dla i = 1: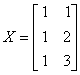 ,
dla i = 2:
,
dla i = 2: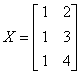 ,
dla i = k – 1:
,
dla i = k – 1: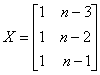 ,
dla i = k:
,
dla i = k: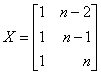 ,
,
y – wektor kolumnowy obserwacji na zmiennej objaśnianej (prognozowanej), i tak (gdy l =3):
dla i = 1: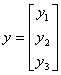 ,
dla i = 2:
,
dla i = 2: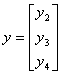 ,
dla i = k –1:
,
dla i = k –1: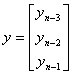 ,
dla i = k:
,
dla i = k: .
.
- Sposób klasyczny ("niemacierzowa" MNK – wzory znane z kursu ekonometrii)

gdzie:
- średnie
arytmetyczne obliczamy ze wzorów:
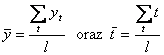 ,
,
- wszelkie sumowania przebiegają po wartościach zmiennej czasowej danego modelu segmentowego.
- Sposób uproszczony – rozwiązujemy układ równań normalnych, pozostawiając nieprzekształcone równania z czterema sumami (uwagi o sumowaniu – jak poprzednio):
(układ równań normalnych)

(... i ostateczne wzory)
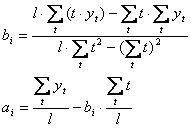
Krok 3. Obliczenie „segmentowych” wartości teoretycznych zmiennej prognozowanej
Dla każdego modelu segmentowego obliczamy l-elementowy ciąg wartości teoretycznych zmiennej prognozowanej a korzystamy ze wzoru:
![]()
w którym ai i bi oznaczają oceny parametrów strukturalnych i-tego modelu segmentowego. Przy założeniu, że l = 3, przebieg obliczeń pokazuje poniższa tabela.
|
i |
Oceny parametrów (ai, bi) |
Wartości zmiennej czasowej (t) |
Wartości teoretyczne i-tego modelu ( |
|
1 |
a1, b1 |
1, 2, 3 |
|
|
2 |
a2, b2 |
2, 3, 4 |
|
|
... |
... |
... |
... |
|
k-1 |
ak-1, bk-1 |
n-3, n-2, n-1 |
|
|
k |
ak, bk |
n-2, n-1, n |
|
Krok 4. Obliczenie ostatecznych wartości teoretycznych zmiennej prognozowanej
W kroku trzecim obliczyliśmy k (bo tyle jest modeli segmentowych) l-elementowych „segmentowych” wartości teoretycznych zmiennej prognozowanej. Aby obliczyć wartości trendu pełzającego, czyli n ostatecznych wartości teoretycznych, należy zastosować podany wzór dla wszystkich t = 1, 2, ..., n:
![]()
gdzie:
![]() -
ostateczna wartość teoretyczna dla okresu lub momentu t,
-
ostateczna wartość teoretyczna dla okresu lub momentu t,
ki - liczba „segmentowych” teoretycznych wartości zmiennej prognozowanej dla okresu lub momentu t,
![]() -
j-ta teoretyczna wartość zmiennej prognozowanej dla okresu lub
momentu t obliczona z i-tego modelu segmentowego.
-
j-ta teoretyczna wartość zmiennej prognozowanej dla okresu lub
momentu t obliczona z i-tego modelu segmentowego.
Przy założeniu, że l = 3, sposób prowadzenia obliczeń pokazuje poniższa tabela.
|
Wartość zmiennej czasowej (t) |
Liczba modeli segmentowych (ki) |
Zbiór numerów modeli segmentowych |
|
|
1 |
1 |
{1} |
|
|
2 |
2 |
{1, 2} |
|
|
3 |
3 |
{1, 2, 3} |
|
|
... |
3 |
... |
... |
|
n-2 |
3 |
{k-2, k-1, k} |
|
|
n-1 |
2 |
{k-1, k} |
|
|
n |
1 |
{k} |
|
Przebieg obliczeń w metodzie trendu pełzającego zilustrujemy przykładem.
Metoda trendu pełzającego (przykład)
Dysponujemy n = 14-elementowym szeregiem czasowym okresów, w którym yt oznacza zaobserwowane roczne wydobycie węgla brunatnego (w mln ton) w pewnym zagłębiu górniczym w Polsce, w latach 1980-1993.
| Lata |
t |
yt |
|
1980 |
1 |
22,6 |
|
1981 |
2 |
24,5 |
|
1982 |
3 |
23,9 |
|
1983 |
4 |
26,9 |
|
1984 |
5 |
30,9 |
|
1985 |
6 |
32,8 |
|
1986 |
7 |
34,5 |
|
1987 |
8 |
38,2 |
|
1988 |
9 |
39,2 |
|
1989 |
10 |
39,8 |
|
1990 |
11 |
39,9 |
|
1991 |
12 |
39,3 |
|
1992 |
13 |
40,8 |
|
1993 |
14 |
41,0 |
Podany szereg czasowy okresów należy wygładzić trendem pełzającym, przyjmując okres wygładzania l = 3 (krok 1 mamy więc za sobą!).
Krok 2. Oszacowanie k liniowych modeli tendencji rozwojowej
k = n - l + 1 = 14 – 3 + 1 = 12
(zastosowano sposób uproszczony)
| Lata |
Numer modelu segmentowego (i) |
Dane |
Obliczenia |
||||||
|
t |
yt |
Suma(yt) |
Suma(yt*t) |
Suma(t) |
Suma(t2) |
ai |
bi |
||
|
1980 |
|
1 |
22,6 |
- |
- |
- |
- |
- |
- |
|
1981 |
1 |
2 |
24,5 |
71,0 |
143,3 |
6,0 |
14,0 |
22,37 |
0,65 |
|
1982 |
2 |
3 |
23,9 |
75,3 |
228,3 |
9,0 |
29,0 |
21,50 |
1,20 |
|
1983 |
3 |
4 |
26,9 |
81,7 |
333,8 |
12,0 |
50,0 |
13,23 |
3,50 |
|
1984 |
4 |
5 |
30,9 |
90,6 |
458,9 |
15,0 |
77,0 |
15,45 |
2,95 |
|
1985 |
5 |
6 |
32,8 |
98,2 |
592,8 |
18,0 |
110,0 |
21,93 |
1,80 |
|
1986 |
6 |
7 |
34,5 |
105,5 |
743,9 |
21,0 |
149,0 |
16,27 |
2,70 |
|
1987 |
7 |
8 |
38,2 |
111,9 |
899,9 |
24,0 |
194,0 |
18,50 |
2,35 |
|
1988 |
8 |
9 |
39,2 |
117,2 |
1056,4 |
27,0 |
245,0 |
31,87 |
0,80 |
|
1989 |
9 |
10 |
39,8 |
118,9 |
1189,7 |
30,0 |
302,0 |
36,13 |
0,35 |
|
1990 |
10 |
11 |
39,9 |
119,0 |
1308,5 |
33,0 |
365,0 |
42,42 |
-0,25 |
|
1991 |
11 |
12 |
39,3 |
120,0 |
1440,9 |
36,0 |
434,0 |
34,60 |
0,45 |
|
1992 |
12 |
13 |
40,8 |
121,1 |
1576,0 |
39,0 |
509,0 |
29,32 |
0,85 |
|
1993 |
|
14 |
41,0 |
- |
- |
- |
- |
- |
- |
Interpretacja uzyskanych ocen parametrów ai i bi:
Każda z k=12 wartości ai oznacza teoretyczną wielkość wydobycia węgla brunatnego dla t = 0 (czyli w 1979 roku), przy założeniu liniowego trendu rozwojowego; i tak:
a1 = 22,37 mln ton, jeśli do obliczeń weźmiemy dane za lata 1980, 1981 i 1982;
a2 = 21,50 mln ton, jeśli do obliczeń weźmiemy dane za lata 1981, 1982 i 1983;
a10 = 42,42 mln ton, jeśli do obliczeń weźmiemy dane za lata 1989, 1990 i 1991;
a12 = 29,32 mln ton, jeśli do obliczeń weźmiemy dane za lata 1991, 1992 i 1993.
Każda z k=12 wartości bi oznacza teoretyczną wielkość przeciętnego rocznego przyrostu bezwzględnego wydobycia węgla brunatnego; i tak:
b1 = 0,65 mln ton (trend wzrostowy), jeśli do obliczeń weźmiemy dane za lata 1980, 1981 i 1982;
b2 = 1,20 mln ton (trend wzrostowy), jeśli do obliczeń weźmiemy dane za lata 1981, 1982 i 1983;
b10 = -0,25 mln ton (trend malejący), jeśli do obliczeń weźmiemy dane za lata 1989, 1990 i 1991;
b12 = 0,85 mln ton (trend wzrostowy), jeśli do obliczeń weźmiemy dane za lata 1991, 1992 i 1993.
Komentarz do obliczeń według wzorów sposobu uproszczonego:
|
i |
Lata |
Dane |
Sumy |
|
1 |
{1980; 1981; 1982} |
t = {1; 2; 3} yt = {22,6; 24,5; 23,9} |
Suma(yt) = 22,6 + 24,5 + 23,9 Suma(yt*t) = 1*22,6 + 2*24,5 + 3*23,9 Suma(t) = 1 + 2 + 3 Suma(t2) = 1 + 4 + 9 |
|
2 |
{1981; 1982; 1983} |
t = {2; 3; 4} yt = {24,5; 23,9; 26,9} |
Suma(yt) = 24,5 + 23,9 + 26,9 Suma(yt*t) = 2*24,5 + 3*23,9 + 4*26,9 Suma(t) = 2 + 3 + 4 Suma(t2) = 4 + 9 + 16 |
|
... |
... |
... |
... |
|
11 |
{1990; 1991; 1992} |
t = {11; 12; 13} yt = {39,9; 39,3; 40,8} |
Suma(yt) = 39,9 + 39,3 + 40,8 Suma(yt*t) = 11*39,9 + 12*39,3 + 13*40,8 Suma(t) = 11 + 12 + 13 Suma(t2) = 121 + 144 + 169 |
|
12 |
{1991; 1992;1993} |
t = {12; 13; 14} yt = {39,3; 40,8; 41,0} |
Suma(yt) = 39,3 + 40,8 + 41,0 Suma(yt*t) = 12*39,3 + 13*40,8 + 14*41,0 Suma(t) = 12 + 13 + 14 Suma(t2) = 144 + 169 + 1196 |
Krok 3.
Obliczenie „segmentowych” wartości teoretycznych zmiennej objaśnianej,
![]()
W tabeli „Obliczone
![]() i
i
![]() ”
są to wartości w kolumnach od „
”
są to wartości w kolumnach od „![]() ”
do „
”
do „![]() ”.Dla
przykładu:
”.Dla
przykładu: ![]() =
22,37 + 0,65*1 = 23,02;
=
22,37 + 0,65*1 = 23,02; ![]() =
22,37 + 0,65 * 2 = 23,67;
=
22,37 + 0,65 * 2 = 23,67; ![]() =
21,50 + 1,20*2 = 23,90;
=
21,50 + 1,20*2 = 23,90; ![]() =
29,32 + 0,85*14 = 41,22 itd., gdyż formułę
=
29,32 + 0,85*14 = 41,22 itd., gdyż formułę
![]()
czytamy: teoretyczna wartość zmiennej objaśnianej w okresie t obliczona na podstawie i-tego modelu segmentowego.
Obliczone
![]() i
i
![]()
| Lata |
t |
yt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1980 |
1 |
22,6 |
23,02 |
|
|
|
|
|
|
|
|
|
|
|
23,02 |
|
1981 |
2 |
24,5 |
23,67 |
23,90 |
|
|
|
|
|
|
|
|
|
|
23,78 |
|
1982 |
3 |
23,9 |
24,32 |
25,10 |
23,73 |
|
|
|
|
|
|
|
|
|
24,38 |
|
1983 |
4 |
26,9 |
|
26,30 |
27,23 |
27,25 |
|
|
|
|
|
|
|
|
26,93 |
|
1984 |
5 |
30,9 |
|
|
30,73 |
30,20 |
30,93 |
|
|
|
|
|
|
|
30,62 |
|
1985 |
6 |
32,8 |
|
|
|
33,15 |
32,73 |
32,47 |
|
|
|
|
|
|
32,78 |
|
1986 |
7 |
34,5 |
|
|
|
|
34,53 |
35,17 |
34,95 |
|
|
|
|
|
34,88 |
|
1987 |
8 |
38,2 |
|
|
|
|
|
37,87 |
37,30 |
38,27 |
|
|
|
|
37,81 |
|
1988 |
9 |
39,2 |
|
|
|
|
|
|
39,65 |
39,07 |
39,28 |
|
|
|
39,33 |
|
1989 |
10 |
39,8 |
|
|
|
|
|
|
|
39,87 |
39,63 |
39,92 |
|
|
39,81 |
|
1990 |
11 |
39,9 |
|
|
|
|
|
|
|
|
39,98 |
39,67 |
39,55 |
|
39,73 |
|
1991 |
12 |
39,3 |
|
|
|
|
|
|
|
|
|
39,42 |
40,00 |
39,52 |
39,64 |
|
1992 |
13 |
40,8 |
|
|
|
|
|
|
|
|
|
|
40,45 |
40,37 |
40,41 |
|
1993 |
14 |
41,0 |
|
|
|
|
|
|
|
|
|
|
|
41,22 |
41,22 |
Krok 4.
Obliczenie ostatecznych wartości teoretycznych zmiennej objaśnianej,
![]()
Wygładzone, ostateczne wartości
teoretyczne zawiera ostatnia kolumna tabeli „Obliczone
 i
i
 ”.
W każdym wierszu, czyli dla każdego t, obliczamy średnie
arytmetyczne z „segmentowych” wartości teoretycznych zmiennej
objaśnianej.
”.
W każdym wierszu, czyli dla każdego t, obliczamy średnie
arytmetyczne z „segmentowych” wartości teoretycznych zmiennej
objaśnianej.
Ekstrapolacja trendu z zastosowaniem wag harmonicznych
Drugi etap metody Hellwiga jest właściwym prognozowaniem. Prognozę punktową obliczamy ze wzoru:
![]()
gdzie:
T – numer okresu lub momentu czasu, dla którego stawiamy prognozę (T > n),
w - współczynnik harmoniczny - najbardziej prawdopodobny jednookresowy przyrost funkcji trendu,
![]() -
teoretyczna ("wygładzona") wartość zmiennej prognozowanej dla ostatniego
elementu szeregu czasowego (przywołujemy przykład –
-
teoretyczna ("wygładzona") wartość zmiennej prognozowanej dla ostatniego
elementu szeregu czasowego (przywołujemy przykład –
![]() =
=
![]() =
41,22).
=
41,22).
Wartość T jest zadawana na wejściu procesu prognozowania, pozostaje więc obliczenie współczynnika harmonicznego, aby wszystko z prawej strony wzoru było wiadome. Oto wzór na współczynnik harmoniczny:
![]()
gdzie ułamek
![]() (dla
t = 1, 2, ..., n-1) nazywamy wagą harmoniczną – stąd
wzięła się nazwa metody prognozowania.
(dla
t = 1, 2, ..., n-1) nazywamy wagą harmoniczną – stąd
wzięła się nazwa metody prognozowania.
Przytoczony wzór ma logiczne
uzasadnienie. Współczynnik w jest po prostu ważoną średnią
arytmetyczną n-1 bezwzględnych przyrostów wartości teoretycznych
zmiennej prognozowanej. Są to kolejno przyrosty: n-1-okresowe,
n-2-okresowe, ..., 2-okresowe i jednookresowy, liczone od okresu
n-tego w przeszłość. Najmniej waży przyrost n-1 okresowy,
najwięcej zaś – przyrost jednookresowy. Jest to realizacja zasady
„starzenia się” informacji. W poniższej tabeli zamieszczono przebieg i
wynik obliczeń sumy
![]() dla
danych z naszego przykładu.
dla
danych z naszego przykładu.
|
Lata |
t |
yt |
|
|
|
|
1980 |
1 |
22,6 |
23,02 |
18,20 |
1,400 (18,20 / 13) |
|
1981 |
2 |
24,5 |
23,78 |
17,43 |
1,453 (17,43 / 12) |
|
1982 |
3 |
23,9 |
24,38 |
16,83 |
1,530 (...) |
|
1983 |
4 |
26,9 |
26,93 |
14,29 |
1,429 |
|
1984 |
5 |
30,9 |
30,62 |
10,59 |
1,177 |
|
1985 |
6 |
32,8 |
32,78 |
8,43 |
1,054 |
|
1986 |
7 |
34,5 |
34,88 |
6,33 |
0,905 |
|
1987 |
8 |
38,2 |
37,81 |
3,41 |
0,568 |
|
1988 |
9 |
39,2 |
39,33 |
1,88 |
0,377 |
|
1989 |
10 |
39,8 |
39,81 |
1,41 |
0,353 |
|
1990 |
11 |
39,9 |
39,73 |
1,48 |
0,494 |
|
1991 |
12 |
39,3 |
39,64 |
1,57 |
0,786 (1,57 / 2) |
|
1992 |
13 |
40,8 |
40,41 |
0,81 |
0,808 (0,81 / 1) |
|
1993 |
14 |
41,0 |
41,22 |
- |
- |
|
|
12,334 |
||||
Ostatecznie...
![]()
Interpretacja: w = 0,949 mln ton - o tyle średnio z roku na rok będzie wzrastało wydobycie węgla brunatnego!
Obliczenie prognozy punktowej
Kontynuujemy przykład z wydobyciem węgla. Należy wyznaczyć prognozy punktowe wydobycia na lata 1994, 1995 i 1996. Wielkości wcześniej obliczone:
w = 0,949,
n = 14 (rok 1993),
![]() =41,22.
=41,22.
Zadajemy odpowiednie wartości parametru T i podstawiamy do wzoru na prognozę punktową – patrz tabela.
| Rok |
T |
|
|
|
1994 |
15 |
0,949*(15-14) + 41,22 = |
42,17 |
|
1995 |
16 |
0,949*(16-14) + 41,22 = |
43,11 |
|
1996 |
17 |
0,949*(17-14) + 41,22 = |
44,06 |
Błąd predykcji punktowej (VT) - podobnie jak w przypadku modelu wyrównania wykładniczego - obliczamy ze wzoru:
VT » Wr
* ![]()
gdzie:
Wr - współczynnik rozbieżności Theila wyznaczany ze wzoru
 ,
,
w którym
![]() oznacza
teoretyczną wartość zmiennej prognozowanej (wyznaczoną według metody
trendu pełzającego) w okresie lub momencie t, dla t = 1,
2, ..., n.
oznacza
teoretyczną wartość zmiennej prognozowanej (wyznaczoną według metody
trendu pełzającego) w okresie lub momencie t, dla t = 1,
2, ..., n.
Współczynnik rozbieżności Theila
zastosowany w prognozowaniu metodą Hellwiga (ściślej: w prognozowaniu
metodą wag harmonicznych) "bierze po uwagę" sumę kwadratów różnic
wartości empirycznych (yt) i wartości teoretycznych (![]() )
zmiennej prognozowanej. Sumę tę odnosi (w sensie ilorazu) do kwadratów
wartości empirycznych (yt). Pierwiastek z tego ilorazu
pozwala obliczyć względny (procentowy) udział błędu predykcji w wartości
punktowej prognozy (
)
zmiennej prognozowanej. Sumę tę odnosi (w sensie ilorazu) do kwadratów
wartości empirycznych (yt). Pierwiastek z tego ilorazu
pozwala obliczyć względny (procentowy) udział błędu predykcji w wartości
punktowej prognozy (![]() ).
Udział ten (procentowo) jest jednakowy dla wszystkich prognoz
punktowych, niezależnie od oddalenia predykcji w przyszłość. Poniższa
tabela obrazuje proces obliczania współczynnika rozbieżności Theila.
).
Udział ten (procentowo) jest jednakowy dla wszystkich prognoz
punktowych, niezależnie od oddalenia predykcji w przyszłość. Poniższa
tabela obrazuje proces obliczania współczynnika rozbieżności Theila.
|
Lata |
t |
yt |
|
|
|
|
1980 |
1 |
22,6 |
23,02 |
0,1764 |
510,76 |
|
1981 |
2 |
24,5 |
23,78 |
0,5184 |
600,25 |
|
1982 |
3 |
23,9 |
24,38 |
0,2304 |
571,21 |
|
1983 |
4 |
26,9 |
26,93 |
0,0009 |
723,61 |
|
1984 |
5 |
30,9 |
30,62 |
0,0784 |
954,81 |
|
1985 |
6 |
32,8 |
32,78 |
0,0004 |
1075,84 |
|
1986 |
7 |
34,5 |
34,88 |
0,1444 |
1190,25 |
|
1987 |
8 |
38,2 |
37,81 |
0,1521 |
1459,24 |
|
1988 |
9 |
39,2 |
39,33 |
0,0169 |
1536,64 |
|
1989 |
10 |
39,8 |
39,81 |
0,0001 |
1584,04 |
|
1990 |
11 |
39,9 |
39,73 |
0,0289 |
1592,01 |
|
1991 |
12 |
39,3 |
39,64 |
0,1156 |
1544,49 |
|
1992 |
13 |
40,8 |
40,41 |
0,1521 |
1664,64 |
|
1993 |
14 |
41,0 |
41,22 |
0,0484 |
1681,00 |
|
Razem |
474,3 |
474,34 |
1,6634 |
16688,79 |
|
|
Średnia |
33,9 |
33,88 |
0,1188 |
1192,06 |
|
![]() =
0,00998 = 0,998%
=
0,00998 = 0,998%
Mamy tutaj do czynienia z niezwykle małą niezgodnością pomiędzy empirycznymi a teoretycznymi wartościami zmiennej prognozowanej. Można stwierdzić, że bardzo dużą zgodnoś
| Rok |
T |
|
|
1994 |
15 |
42,17 |
|
1995 |
16 |
43,11 |
|
1996 |
17 |
44,06 |
Jeżeli zaś chodzi o prognozowanie przedziałowe, to postępujemy dokładnie tak samo jak w przypadku prognozowania na podstawie modelu wyrównania wykładniczego.